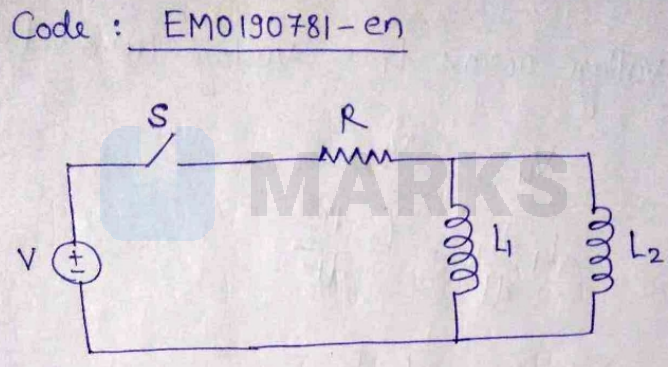
As ${\mathrm{L}}_1$ and ${\mathrm{L}}_2$ are in parallel so equivalent  

inductance, $\mathrm{L}=\frac{{\mathrm{L}}_1{\mathrm{L}}_2}{{\mathrm{L}}_1+{\mathrm{L}}_2}$

Here, $L_1$ and $L_2$ are the inductance (shown in circuit)

The current through the $\mathrm{RL}$ series circuit at anytime is given as 

$\mathrm{I}=\mathrm{ }\frac{\mathrm{V}}{\mathrm{R}}\left(1-{\mathrm{e}}^{\frac{-\mathrm{Rt}}{\mathrm{L}}}\right)$

At $\mathrm{t}=0$,

$\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}}\left(1-{\mathrm{e}}^0\right)=0$

After a longtime i.e. at $\mathrm{t}=\infty$

$\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}}\left(1-{\mathrm{e}}^{-\infty }\right)$

$\Rightarrow \mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}}$

Let currents through ${\mathrm{L}}_1$ and ${\mathrm{L}}_2$ are ${\mathrm{I}}_1$ and ${\mathrm{I}}_2$ respectively. As ${\mathrm{L}}_1$ and ${\mathrm{L}}_2$ are joined in parallel

Voltage across ${\mathrm{L}}_1=$ Voltage across ${\mathrm{L}}_2$

$\Rightarrow {\mathrm{V}}_{{\mathrm{L}}_1}={\mathrm{V}}_{{\mathrm{L}}_2}$

$\Rightarrow {\mathrm{L}}_1\frac{d{\mathrm{I}}_1}{d\mathrm{t}}={\mathrm{L}}_2\frac{d{\mathrm{I}}_2}{d\mathrm{t}}$

$\Rightarrow {\mathrm{L}}_1{\mathrm{I}}_1={\mathrm{L}}_2{\mathrm{I}}_2$

Thus, $\frac{{\mathrm{I}}_1}{{\mathrm{I}}_2}=\frac{{\mathrm{L}}_2}{{\mathrm{L}}_1}$

By current division rule,

Current ${\mathrm{I}}_1$ across ${\mathrm{L}}_1$ is 

${\mathrm{I}}_1=\frac{{\mathrm{L}}_2}{{\mathrm{L}}_1+{\mathrm{L}}_2}\times \mathrm{I}$

$\Rightarrow {\mathrm{I}}_1=\frac{\mathrm{V}}{\mathrm{R}}\left(\frac{{\mathrm{L}}_2}{{\mathrm{L}}_1+{\mathrm{L}}_2}\right)$

Current ${\mathrm{I}}_2$ across ${\mathrm{L}}_2$ is

${\mathrm{I}}_2=\frac{{\mathrm{L}}_1}{{\mathrm{L}}_1+{\mathrm{l}}_2}\times \mathrm{I}$

${\mathrm{I}}_2=\frac{\mathrm{V}}{\mathrm{R}}\left(\frac{{\mathrm{L}}_1}{{\mathrm{L}}_1+{\mathrm{L}}_2}\right)$