Paragraph: Consider a simple \(R C\) circuit as shown in Figure \(1\). Process...
Paragraph:
Consider a simple \(R C\) circuit as shown in Figure \(1\).
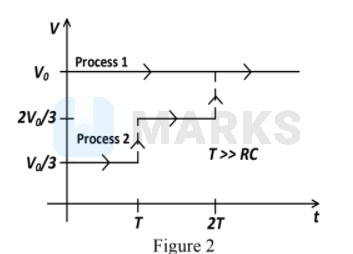
Process 1: In the circuit the switch \(S\) is closed at \(t=0\) and the capacitor is fully charged to voltage \(V_{0}\) (i.e., charging continues for time \(T>>R C\) ). In the process some dissipation \(\left(E_{D}\right)\) occurs across the resistance \(R\). The amount of energy finally stored in the fully charged capacitor is \(E_{C}\).
Process 2: In a different process the voltage is first set to \(\frac{V_{0}}{3}\) and maintained for a charging time \(T>>R C\). Then the voltage is raised to \(\frac{2 V_{0}}{3}\) without discharging the capacitor and again maintained for a time \(T>>R C\). The process is repeated one more time by raising the voltage to \(V_{0}\) and the capacitor is charged to the same final voltage \(V_{0}\) as in Process 1.
These two processes are depicted in Figure \(2 .\)

Question:
In Process 1 , the energy stored in the capacitor \(E_{C}\) and heat dissipated across resistance \(E_{D}\) are related by:
Consider a simple \(R C\) circuit as shown in Figure \(1\).
Process 1: In the circuit the switch \(S\) is closed at \(t=0\) and the capacitor is fully charged to voltage \(V_{0}\) (i.e., charging continues for time \(T>>R C\) ). In the process some dissipation \(\left(E_{D}\right)\) occurs across the resistance \(R\). The amount of energy finally stored in the fully charged capacitor is \(E_{C}\).
Process 2: In a different process the voltage is first set to \(\frac{V_{0}}{3}\) and maintained for a charging time \(T>>R C\). Then the voltage is raised to \(\frac{2 V_{0}}{3}\) without discharging the capacitor and again maintained for a time \(T>>R C\). The process is repeated one more time by raising the voltage to \(V_{0}\) and the capacitor is charged to the same final voltage \(V_{0}\) as in Process 1.
These two processes are depicted in Figure \(2 .\)


Question:
In Process 1 , the energy stored in the capacitor \(E_{C}\) and heat dissipated across resistance \(E_{D}\) are related by:
Solution:

When switch is closed for a very long time capacitor will get fully charged and charge on capacitor will be
Energy stored in capacitor .....(i)
Work done by battery
Dissipated across resistance = (work done by battery) – (energy store)
.....(ii)
From (i) and (ii)

When switch is closed for a very long time capacitor will get fully charged and charge on capacitor will be
Energy stored in capacitor .....(i)
Work done by battery
Dissipated across resistance = (work done by battery) – (energy store)
.....(ii)
From (i) and (ii)
















 JEE Main
JEE Main JEE Advanced
JEE Advanced NEET UG
NEET UG BITSAT
BITSAT COMEDK
COMEDK VITEEE
VITEEE WBJEE
WBJEE
Join the conversation